Embedding

Canonical Correlation Analysis (CCA)

class mvlearn.embed.CCA(n_components=1, regs=None, signal_ranks=None, center=True, i_mcca_method='auto', multiview_output=True)

Canonical Correlation Analysis (CCA)

CCA inherits from MultiCCA (MCCA) but is restricted to 2 views which allows for certain statistics to be computed about the results.

Parameters

• n_components (int (default 1)) -- Number of canonical components to compute and return.

• regs (float | 'lw' | 'oas' | None, or list, optional (default None)) --

  CCA regularization for each data view, which can be important for high dimensional data. A list will specify for each view separately. If float, must be between 0 and 1 (inclusive).

  • 0 or None : corresponds to SUMCORR-AVGVAR MCCA.

  • 1 : partial least squares SVD (generalizes to more than 2 views)

  • 'lw' : Default sklearn.covariance.ledoit_wolf regularization

  • 'oas' : Default sklearn.covariance.oas regularization

• signal_ranks (int, None or list, optional (default None)) -- The initial signal rank to compute. If None, will compute the full SVD. A list will specify for each view separately.

• center (bool, or list (default True)) -- Whether or not to initially mean center the data. A list will specify for each view separately.

• i_mcca_method ('auto' | 'svd' | 'gevp' (default 'auto')) -- Whether or not to use the SVD based method (only works with no regularization) or the gevp based method for informative MCCA.

• multiview_output (bool, optional (default True)) -- If True, the .transform method returns one dataset per view. Otherwise, it returns one dataset, of shape (n_samples, n_components)

means_

The means of each view, each of shape (n_features,)

Type

list of numpy.ndarray

loadings_

The loadings for each view used to project new data, each of shape (n_features_b, n_components).

Type

list of numpy.ndarray

common_score_norms_

Column norms of the sum of the fitted view scores. Used for projecting new data

Type

numpy.ndarray, shape (n_components,)

evals_

The generalized eigenvalue problem eigenvalues.

Type

numpy.ndarray, shape (n_components,)

n_views_

The number of views

Type

int

n_features_

The number of features in each fitted view

Type

list

n_components_

The number of components in each transformed view

Type

int

See also

MCCA, KMCCA

References

1

Kettenring, J. R., "Canonical Analysis of Several Sets of Variables." Biometrika, 58:433-451, (1971)

2

Tenenhaus, A., et al. "Regularized generalized canonical correlation analysis." Psychometrika, 76:257–284, 2011

Examples

>>> from mvlearn.embed import CCA
>>> X1 = [[0., 0., 1.], [1.,0.,0.], [2.,2.,2.], [3.,5.,4.]]
>>> X2 = [[0.1, -0.2], [0.9, 1.1], [6.2, 5.9], [11.9, 12.3]]
>>> cca = CCA()
>>> cca.fit([X1, X2])
CCA()
>>> Xs_scores = cca.transform([X1, X2])

Multiview Canonical Correlation Analysis (MCCA)

class mvlearn.embed.MCCA(n_components=1, regs=None, signal_ranks=None, center=True, i_mcca_method='auto', multiview_output=True)

Multiview canonical correlation analysis for any number of views. Includes options for regularized MCCA and informative MCCA (where a low rank PCA is first computed).

Parameters

• n_components (int | 'min' | 'max' | None (default 1)) -- Number of final components to compute. If int, will compute that many. If None, will compute as many as possible. 'min' and 'max' will respectively use the minimum/maximum number of features among views.

• regs (float | 'lw' | 'oas' | None, or list, optional (default None)) --

  MCCA regularization for each data view, which can be important for high dimensional data. A list will specify for each view separately. If float, must be between 0 and 1 (inclusive).

  • 0 or None : corresponds to SUMCORR-AVGVAR MCCA.

  • 1 : partial least squares SVD (generalizes to more than 2 views)

  • 'lw' : Default sklearn.covariance.ledoit_wolf regularization

  • 'oas' : Default sklearn.covariance.oas regularization

• signal_ranks (int, None or list, optional (default None)) -- The initial signal rank to compute. If None, will compute the full SVD. A list will specify for each view separately.

• center (bool, or list (default True)) -- Whether or not to initially mean center the data. A list will specify for each view separately.

• i_mcca_method ('auto' | 'svd' | 'gevp' (default 'auto')) -- Whether or not to use the SVD based method (only works with no regularization) or the gevp based method for informative MCCA.

• multiview_output (bool, optional (default True)) -- If True, the .transform method returns one dataset per view. Otherwise, it returns one dataset, of shape (n_samples, n_components)

means_

The means of each view, each of shape (n_features,)

Type

list of numpy.ndarray

loadings_

The loadings for each view used to project new data, each of shape (n_features_b, n_components).

Type

list of numpy.ndarray

common_score_norms_

Column norms of the sum of the fitted view scores. Used for projecting new data

Type

numpy.ndarray, shape (n_components,)

evals_

The generalized eigenvalue problem eigenvalues.

Type

numpy.ndarray, shape (n_components,)

n_views_

The number of views

Type

int

n_features_

The number of features in each fitted view

Type

list

n_components_

The number of components in each transformed view

Type

int

See also

KMCCA

References

3

Kettenring, J. R., "Canonical Analysis of Several Sets of Variables." Biometrika, 58:433-451, (1971)

4

Tenenhaus, A., et al. "Regularized generalized canonical correlation analysis." Psychometrika, 76:257–284, 2011

Examples

>>> from mvlearn.embed import MCCA
>>> X1 = [[0, 0, 1], [1, 0, 0], [2, 2, 2], [3, 5, 4]]
>>> X2 = [[0.1, -0.2], [0.9, 1.1], [6.2, 5.9], [11.9, 12.3]]
>>> X3 = [[0, 1, 0], [1, 9, 0], [4, 3, 3,], [12, 8, 10]]
>>> mcca = MCCA()
>>> mcca.fit([X1, X2, X3])
MCCA()
>>> Xs_scores = mcca.transform([X1, X2, X3])

Kernel MCCA

class mvlearn.embed.KMCCA(n_components=1, kernel='linear', kernel_params={}, regs=None, signal_ranks=None, sval_thresh=0.001, diag_mode='A', center=True, filter_params=False, n_jobs=None, multiview_output=True, pgso=False, tol=0.1)

Kernel multi-view canonical correlation analysis.

Parameters

• n_components (int, None (default 1)) -- Number of components to compute. If None, will use the number of features.

• kernel (str, callable, or list (default 'linear')) -- The kernel function to use. This is the metric argument to sklearn.metrics.pairwise.pairwise_kernels. A list will specify for each view separately.

• kernel_params (dict, or list (default {})) -- Key word arguments to sklearn.metrics.pairwise.pairwise_kernels. A list will specify for each view separately.

• regs (float, None, or list, optional (default None)) -- None equates to 0. Floats are nonnegative. The value is used to regularize singular values in each view based on diag_mode A list will specify the method for each view separately.

• signal_ranks (int, None, or list, optional (default None)) -- Largest SVD rank to compute for each view. If None, the full rank decomposition will be used. A list will specify for each view separately.

• sval_thresh (float, or list (default 1e-3)) -- For each view we throw out singular values of (1/n)K, the gram matrix scaled by n_samples, below this threshold. A non-zero value deals with singular gram matrices.

• diag_mode ('A' | 'B' | 'C' (default 'A')) --

  Method of regularizing singular values s with regularization parameter r

  • 'A' : \((1 - r) * K^2 + r * K\) 5

  • 'B' : \((1-r) (K + n/2 \kappa * I)^2\) where \(\kappa = r / (1 - r)\) 6

  • 'C' : \((1 - r) K^2 + r * I_n\) 7

• center (bool, or list (default True)) -- Whether or not to initially mean center the data. A list will specify for each view separately.

• filter_params (bool (default False)) -- See sklearn.metrics.pairwise.pairwise_kernels documentation.

• n_jobs (int, None, optional (default None)) -- Number of jobs to run in parallel when computing kernel matrices. See sklearn.metrics.pairwise.pairwise_kernels documentation.

• multiview_output (bool, optional (default True)) -- If True, the .transform method returns one dataset per view. Otherwise, it returns one dataset, of shape (n_samples, n_components)

• pgso (bool, optional (default False)) -- If True, computes a partial Gram-Schmidt orthogonalization approximation of the kernel matrices to the given tolerance.

• tol (float (default 0.1)) -- The minimum matrix trace difference between a kernel matrix and its computed pgso approximation, relative to the kernel trace.

kernel_col_means_

The column means of each gram matrix

Type

list of numpy.ndarray, shape (n_samples,)

kernel_mat_means_

The total means of each gram matrix

Type

list

dual_vars_

The loadings for the gram matrix of each view

Type

numpy.ndarray, shape (n_views, n_samples, n_components)

common_score_norms_

Column norms of the sum of the view scores. Useful for projecting new data

Type

numpy.ndarray, shape (n_components,)

evals_

The generalized eigenvalue problem eigenvalues.

Type

numpy.ndarray, shape (n_components,)

Xs_

• Xs[i] shape (n_samples, n_features_i)

The original data matrices for use in kernel matrix computation during calls to .transform.

Type

list of numpy.ndarray, length (n_views,)

n_views_

The number of views

Type

int

n_features_

The number of features in each fitted view

Type

list

n_components_

The number of components in each transformed view

Type

int

pgso_Ls_

• pgso_Ls_[i] shape (n_samples, rank_i)

The Gram-Schmidt approximations of the kernel matrices

Type

list of numpy.ndarray, length (n_views,)

pgso_norms_

• pgso_norms_[i] shape (rank_i,)

The maximum norms found during the Gram-Schmidt procedure, descending

Type

list of numpy.ndarray, length (n_views,)

pgso_idxs_

• pgso_idxs_[i] shape (rank_i,)

The sample indices of the maximum norms

Type

list of numpy.ndarray, length (n_views,)

pgso_Xs_

• pgso_Xs_[i] shape (rank_i, n_features)

The samples with indices saved in pgso_idxs_, sorted by pgso_norms_

Type

list of numpy.ndarray, length (n_views,)

pgso_ranks_

The ranks of the partial Gram-Schmidt results for each view.

Type

list, length (n_views,)

Notes

Traditional CCA aims to find useful projections of features in each view of data, computing a weighted sum, but may not extract useful descriptors of the data because of its linearity. KMCCA offers an alternative solution by first projecting the data onto a higher dimensional feature space.

\[\phi: \mathbf{x} = (x_1,...,x_m) \mapsto \phi(\mathbf{x}) = (z_1,...,z_N), (m << N)\]

before performing CCA in the new feature space.

Kernels are effectively distance functions that compute inner products in the higher dimensional feature space, a method known as the kernel trick. A kernel function K, such that for all \(\mathbf{x}, \mathbf{z} \in X\)

\[K(\mathbf{x}, \mathbf{z}) = \langle\phi(\mathbf{x}) \cdot \phi(\mathbf{z})\rangle.\]

The kernel matrix \(K_i\) has entries computed from the kernel function. Using the kernel trick, loadings of the kernel matrix (dual_vars_) are solved for rather than of the features from \(\phi\).

Kernel matrices grow exponentially with the size of data. They not only have to store \(n^2\) elements, but also face the complexity of matrix eigenvalue problems. In a Cholesky decomposition a positive definite matrix K is decomposed to a lower triangular matrix \(L\) : \(K = LL'\).

The dual partial Gram-Schmidt orthogonalization (PSGO) is equivalent to the Incomplete Cholesky Decomposition (ICD) which looks for a low rank approximation of \(L\), reducing the cost of operations of the matrix such that \(\frac{1}{\sum_i K_{ii}} tr(K - LL^T) \leq tol\).

A PSGO tolerance yielding rank \(m\) leads to storage requirements of \(O(mn)\) instead of \(O(n^2)\) and becomes \(O(nm^2)\) instead of \(O(n^3)\) 7.

See also

MCCA

References

5

Hardoon D., et al. "Canonical Correlation Analysis: An Overview with Application to Learning Methods", Neural Computation, Volume 16 (12), pp 2639-2664, 2004.

6

Bach, F. and Jordan, M. "Kernel Independent Component Analysis." Journal of Machine Learning Research, 3:1-48, 2002.

7(1,2)

Kuss, M. and Graepel, T.. "The Geometry of Kernel Canonical Correlation Analysis." MPI Technical Report, 108. (2003).

Examples

>>> from mvlearn.embed import KMCCA
>>> X1 = [[0, 0, 1], [1, 0, 0], [2, 2, 2], [3, 5, 4]]
>>> X2 = [[0.1, -0.2], [0.9, 1.1], [6.2, 5.9], [11.9, 12.3]]
>>> X3 = [[0, 1, 0], [1, 9, 0], [4, 3, 3,], [12, 8, 10]]
>>> kmcca = KMCCA()
>>> kmcca.fit([X1, X2, X3])
KMCCA()
>>> Xs_scores = kmcca.transform([X1, X2, X3])

Generalized Canonical Correlation Analysis (GCCA)

class mvlearn.embed.GCCA(n_components=None, fraction_var=None, sv_tolerance=None, n_elbows=2, tall=False, max_rank=False, n_jobs=None)

An implementation of Generalized Canonical Correlation Analysis 8 suitable for cases where the number of features exceeds the number of samples by first applying single view dimensionality reduction. Computes individual projections into a common subspace such that the correlations between pairwise projections are minimized (ie. maximize pairwise correlation). An important note: this is applicable to any number of views, not just two.

Parameters

• n_components (int (positive), optional, default=None) -- If self.sv_tolerance=None, selects the number of SVD components to keep for each view. If none, another selection method is used.

• fraction_var (float, default=None) -- If self.sv_tolerance=None, and self.n_components=None, selects the number of SVD components to keep for each view by capturing enough of the variance. If none, another selection method is used.

• sv_tolerance (float, optional, default=None) -- Selects the number of SVD components to keep for each view by thresholding singular values. If none, another selection method is used.

• n_elbows (int, optional, default: 2) -- If self.fraction_var=None, self.sv_tolerance=None, and self.n_components=None, then compute the optimal embedding dimension using utils.select_dimension(). Otherwise, ignored.

• tall (boolean, default=False) -- Set to true if n_samples > n_features, speeds up SVD

• max_rank (boolean, default=False) -- If true, sets the rank of the common latent space as the maximum rank of the individual spaces. If false, uses the minimum individual rank.

• n_jobs (int (positive), default=None) -- The number of jobs to run in parallel when computing the SVDs for each view in fit and partial_fit. None means 1 job, -1 means using all processors.

projection_mats_

A projection matrix for each view, from the given space to the latent space

Type

list of arrays

ranks_

Number of left singular vectors kept for each view during the first SVD

Type

list of ints

Notes

Consider two views \(X_1\) and \(X_2\). Canonical Correlation Analysis seeks to find vectors \(a_1\) and \(a_2\) to maximize the correlation \(X_1 a_1\) and \(X_2 a_2\), expanded below.

\[\left(\frac{a_1^TC_{12}a_2} {\sqrt{a_1^TC_{11}a_1a_2^TC_{22}a_2}} \right)\]

where \(C_{11}\), \(C_{22}\), and \(C_{12}\) are respectively the view 1, view 2, and between view covariance matrix estimates. GCCA maximizes the sum of these correlations across all pairwise views and computes a set of linearly independent components. This specific algorithm first applies principal component analysis (PCA) independently to each view and then aligns the most informative projections to find correlated and informative subspaces. Parameters that control the embedding dimension apply to the PCA step. The dimension of each aligned subspace is the maximum or minimum of the individual dimensions, per the max_ranks parameter. Using the maximum will capture the most information from all views but also noise from some views. Using the minimum will better remove noise dimensions but at the cost of information from some views.

References

8

B. Afshin-Pour, G.A. Hossein-Zadeh, S.C. Strother, H. Soltanian-Zadeh. "Enhancing reproducibility of fMRI statistical maps using generalized canonical correlation analysis in NPAIRS framework." Neuroimage, volume 60, pp. 1970-1981, 2012

Examples

>>> from mvlearn.datasets import load_UCImultifeature
>>> from mvlearn.embed import GCCA
>>> # Load full dataset, labels not needed
>>> Xs, _ = load_UCImultifeature()
>>> gcca = GCCA(fraction_var = 0.9)
>>> # Transform the first 5 views
>>> Xs_latents = gcca.fit_transform(Xs[:5])
>>> print([X.shape[1] for X in Xs_latents])
[9, 9, 9, 9, 9]

Deep Canonical Correlation Analysis (DCCA)

class mvlearn.embed.DCCA(input_size1=None, input_size2=None, n_components=2, layer_sizes1=None, layer_sizes2=None, use_all_singular_values=False, device=device(type='cpu'), epoch_num=200, batch_size=800, learning_rate=0.001, reg_par=1e-05, tolerance=0.001, print_train_log_info=False)

An implementation of Deep Canonical Correlation Analysis 9 with PyTorch. It computes projections into a common subspace in order to maximize the correlation between pairwise projections into the subspace from two views of data. To obtain these projections, two fully connected deep networks are trained to initially transform the two views of data. Then, the transformed data is projected using linear CCA. This can be thought of as training a kernel for each view that initially acts on the data before projection. The networks are trained to maximize the ability of the linear CCA to maximize the correlation between the final dimensions.

Parameters

• input_size1 (int (positive)) -- The dimensionality of the input vectors in view 1.

• input_size2 (int (positive)) -- The dimensionality of the input vectors in view 2.

• n_components (int (positive), default=2) -- The output dimensionality of the correlated projections. The deep network wil transform the data to this size. Must satisfy: n_components <= max(layer_sizes1[-1], layer_sizes2[-1]).

• layer_sizes1 (list of ints, default=None) -- The sizes of the layers of the deep network applied to view 1 before CCA. For example, if the input dimensionality is 256, and there is one hidden layer with 1024 units and the output dimensionality is 100 before applying CCA, layer_sizes1=[1024, 100]. If None, set to [1000, self.n_components_].

• layer_sizes2 (list of ints, default=None) -- The sizes of the layers of the deep network applied to view 2 before CCA. Does not need to have the same hidden layer architecture as layer_sizes1, but the final dimensionality must be the same. If None, set to [1000, self.n_components_].

• use_all_singular_values (boolean (default=False)) -- Whether or not to use all the singular values in the CCA computation to calculate the loss. If False, only the top n_components singular values are used.

• device (string, default='cpu') -- The torch device for processing. Can be used with a GPU if available.

• epoch_num (int (positive), default=200) -- The max number of epochs to train the deep networks.

• batch_size (int (positive), default=800) -- Batch size for training the deep networks.

• learning_rate (float (positive), default=1e-3) -- Learning rate for training the deep networks.

• reg_par (float (positive), default=1e-5) -- Weight decay parameter used in the RMSprop optimizer.

• tolerance (float, (positive), default=1e-2) -- Threshold difference between successive iteration losses to define convergence and stop training.

• print_train_log_info (boolean, default=False) -- If True, the training loss at each epoch will be printed to the console when DCCA.fit() is called.

input_size1_

The dimensionality of the input vectors in view 1.

Type

int (positive)

input_size2_

The dimensionality of the input vectors in view 2.

Type

int (positive)

n_components_

The output dimensionality of the correlated projections. The deep network wil transform the data to this size. If not specified, will be set to 2.

Type

int (positive)

layer_sizes1_

The sizes of the layers of the deep network applied to view 1 before CCA. For example, if the input dimensionality is 256, and there is one hidden layer with 1024 units and the output dimensionality is 100 before applying CCA, layer_sizes1=[1024, 100].

Type

list of ints

layer_sizes2_

The sizes of the layers of the deep network applied to view 2 before CCA. Does not need to have the same hidden layer architecture as layer_sizes1, but the final dimensionality must be the same.

Type

list of ints

device_

The torch device for processing.

Type

string

batch_size_

Batch size for training the deep networks.

Type

int (positive)

learning_rate_

Learning rate for training the deep networks.

Type

float (positive)

reg_par_

Weight decay parameter used in the RMSprop optimizer.

Type

float (positive)

deep_model_

2 view Deep CCA object used to transform 2 views of data together.

Type

DeepPairedNetworks object

linear_cca_

Linear CCA object used to project final transformations from output of deep_model to the n_components.

Type

linear_cca object

model_

Wrapper around deep_model to allow parallelisation.

Type

torch.nn.DataParallel object

loss_

Loss function for deep_model. Defined as the negative correlation between outputs of transformed views.

Type

cca_loss object

optimizer_

Optimizer used to train the networks.

Type

torch.optim.RMSprop object

Raises

ModuleNotFoundError -- In order to run DCCA, pytorch and other certain optional dependencies must be installed. See the installation page for details.

Notes

Deep Canonical Correlation Analysis is a method of finding highly correlated subspaces for 2 views of data using nonlinear transformations learned by deep networks. It can be thought of as using deep networks to learn the best potentially nonlinear kernels for a variant of kernel CCA.

The networks used for each view in DCCA consist of fully connected linear layers with a sigmoid activation function.

The problem DCCA problem is formulated from 9. Consider two views \(X_1\) and \(X_2\). DCCA seeks to find the parameters for each view, \(\Theta_1\) and \(\Theta_2\), such that they maximize

\[\text{corr}\left(f_1\left(X_1;\Theta_1\right), f_2\left(X_2;\Theta_2\right)\right)\]

These parameters are estimated in the deep network by following gradient descent on the input data. Taking \(H_1, H_2 \in R^{o \times m}\) to be the outputs of the deep network in each column for the input data of size \(m\). Take the centered matrix \(\bar{H}_1 = H_1-\frac{1}{m}H_1{1}\), and \(\bar{H}_2 = H_2-\frac{1}{m}H_2{1}\). Then, define

\[\begin{split}\begin{align*} \hat{\Sigma}_{12} &= \frac{1}{m-1}\bar{H}_1\bar{H}_2^T \\ \hat{\Sigma}_{11} &= \frac{1}{m-1}\bar{H}_1\bar{H}_1^T + r_1I \\ \hat{\Sigma}_{22} &= \frac{1}{m-1}\bar{H}_2\bar{H}_2^T + r_2I \end{align*}\end{split}\]

Where \(r_1\) and \(r_2\) are regularization constants \(>0\) so the matrices are guaranteed to be positive definite.

The correlation objective function is the sum of the top \(k\) singular values of the matrix \(T\), where

\[T = \hat{\Sigma}_{11}^{-1/2}\hat{\Sigma}_{12}\hat{\Sigma}_{22}^{-1/2}\]

Which is the matrix norm of T. Thus, the loss is

\[L(X_1, X2) = -\text{corr}\left(H_1, H_2\right) = -\text{tr}(T^TT)^{1/2}.\]

Examples

>>> from mvlearn.embed import DCCA
>>> import numpy as np
>>> # Exponential data as example of finding good correlation
>>> view1 = np.random.normal(loc=2, size=(1000, 75))
>>> view2 = np.exp(view1)
>>> view1_test = np.random.normal(loc=2, size=(200, 75))
>>> view2_test = np.exp(view1_test)
>>> input_size1, input_size2 = 75, 75
>>> n_components = 2
>>> layer_sizes1 = [1024, 4]
>>> layer_sizes2 = [1024, 4]
>>> dcca = DCCA(input_size1, input_size2, n_components, layer_sizes1,
...             layer_sizes2)
>>> dcca = dcca.fit([view1, view2])
>>> outputs = dcca.transform([view1_test, view2_test])
>>> print(outputs[0].shape)
(200, 2)

References

9(1,2,3)

Andrew, G., et al., "Deep canonical correlation analysis." In Proceedings of the 30th International Conference on International Conferenceon Machine Learning, volume 28, pages 1247–1255. JMLR.org, 2013.

Multiview Multidimensional Scaling

class mvlearn.embed.MVMDS(n_components=2, num_iter=15, dissimilarity='euclidean')

An implementation of Classical Multiview Multidimensional Scaling for jointly reducing the dimensions of multiple views of data 10. A Euclidean distance matrix is created for each view, double centered, and the k largest common eigenvectors between the matrices are found based on the stepwise estimation of common principal components. Using these common principal components, the views are jointly reduced and a single view of k-dimensions is returned.

MVMDS is often a better alternative to PCA for multi-view data. See the tutorials in the documentation.

Parameters

• n_components (int (positive), default=2) -- Represents the number of components that the user would like to be returned from the algorithm. This value must be greater than 0 and less than the number of samples within each view.

• num_iter (int (positive), default=15) -- Number of iterations stepwise estimation goes through.

• dissimilarity ({'euclidean', 'precomputed'}, default='euclidean') --

  Dissimilarity measure to use:

  'euclidean': Pairwise Euclidean distances between points in the dataset.

  'precomputed': Xs is treated as pre-computed dissimilarity matrices.

components_

Joint transformed MVMDS components of the input views.

Type

numpy.ndarray, shape(n_samples, n_components)

Notes

Classical Multiview Multidimensional Scaling can be broken down into two steps. The first step involves calculating the Euclidean Distance matrices, \(Z_i\), for each of the \(k\) views and double-centering these matrices through the following calculations:

\[\Sigma_{i}=-\frac{1}{2}J_iZ_iJ_i\]

\[\text{where }J_i=I_i-{\frac {1}{n}}\mathbb{1}\mathbb{1}^T\]

The second step involves finding the common principal components of the \(\Sigma\) matrices. These can be thought of as multiview generalizations of the principal components found in principal component analysis (PCA) given several covariance matrices. The central hypothesis of the common principal component model states that given k normal populations (views), their \(p\) x \(p\) covariance matrices \(\Sigma_{i}\), for \(i = 1,2,...,k\) are simultaneously diagonalizable as:

\[\Sigma_{i} = QD_i^2Q^T\]

where \(Q\) is the common \(p\) x \(p\) orthogonal matrix and \(D_i^2\) are positive \(p\) x \(p\) diagonal matrices. The \(Q\) matrix contains all the common principal components. The common principal component, \(q_j\), is found by solving the minimization problem:

\[\text{Minimize} \sum_{i=1}^{k}n_ilog(q_j^TS_iq_j)\]

\[\text{Subject to } q_j^Tq_j = 1\]

where \(n_i\) represent the degrees of freedom and \(S_i\) represent sample covariance matrices.

This class does not support MVMDS.transform() due to the iterative nature of the algorithm and the fact that the transformation is done during iterative fitting. Use MVMDS.fit_transform() to do both fitting and transforming at once.

Examples

>>> from mvlearn.embed import MVMDS
>>> from mvlearn.datasets import load_UCImultifeature
>>> Xs, _ = load_UCImultifeature()
>>> print(len(Xs)) # number of samples in each view
6
>>> print(Xs[0].shape) # number of samples in each view
(2000, 76)
>>> mvmds = MVMDS(n_components=5)
>>> Xs_reduced = mvmds.fit_transform(Xs)
>>> print(Xs_reduced.shape)
(2000, 5)

References

10

Trendafilov, Nickolay T. “Stepwise Estimation of Common Principal Components.” Computational Statistics & Data Analysis, 54(12):3446–3457, 2010

11

Kanaan-Izquierdo, Samir, et al. "Multiview: a software package for multiview pattern recognition methods." Bioinformatics, 35(16):2877–2879, 2019

Split Autoencoder

class mvlearn.embed.SplitAE(hidden_size=64, num_hidden_layers=2, embed_size=20, training_epochs=10, batch_size=16, learning_rate=0.001, print_info=False, print_graph=True)

Implements an autoencoder that creates an embedding of a view View1 and from that embedding reconstructs View1 and another view View2, as described in 12.

Parameters

• hidden_size (int (default=64)) -- number of nodes in the hidden layers

• num_hidden_layers (int (default=2)) -- number of hidden layers in each encoder or decoder net

• embed_size (int (default=20)) -- size of the bottleneck vector in the autoencoder

• training_epochs (int (default=10)) -- how many times the network trains on the full dataset

• batch_size (int (default=16):) -- batch size while training the network

• learning_rate (float (default=0.001)) -- learning rate of the Adam optimizer

• print_info (bool (default=False)) -- whether or not to print errors as the network trains.

• print_graph (bool (default=True)) -- whether or not to graph training loss

view1_encoder_

the View1 embedding network as a PyTorch module

Type

torch.nn.Module

view1_decoder_

the View1 decoding network as a PyTorch module

Type

torch.nn.Module

view2_decoder_

the View2 decoding network as a PyTorch module

Type

torch.nn.Module

Raises

ModuleNotFoundError -- In order to run SplitAE, pytorch and other certain optional dependencies must be installed. See the installation page for details.

Notes

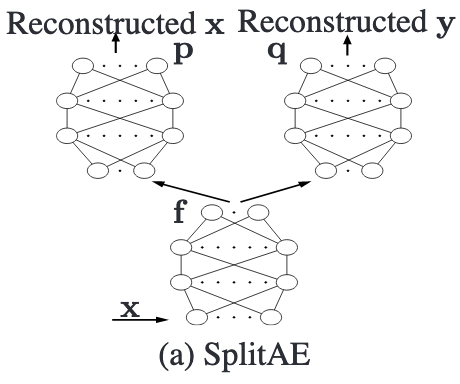
In this figure \(\textbf{x}\) is View1 and \(\textbf{y}\) is View2

Each encoder / decoder network is a fully connected neural net with paramater count equal to:

\[\left(\text{input_size} + \text{embed_size}\right) \cdot \text{hidden_size} + \sum_{1}^{\text{num_hidden_layers}-1}\text{hidden_size}^2\]

Where \(\text{input_size}\) is the number of features in View1 or View2.

The loss that is reduced via gradient descent is:

\[J = \left(p(f(\textbf{x})) - \textbf{x}\right)^2 + \left(q(f(\textbf{x})) - \textbf{y}\right)^2\]

Where \(f\) is the encoder, \(p\) and \(q\) are the decoders, \(\textbf{x}\) is View1, and \(\textbf{y}\) is View2.

References

12

Wang, Weiran, et al. "On Deep Multi-View Representation Learning." In Proceedings of the 32nd International Conference on Machine Learning, 37:1083-1092, 2015.

For more extensive examples, see the tutorials for SplitAE in this documentation.

DCCA Utilities

class mvlearn.embed.linear_cca

Implementation of linear CCA to act on the output of the deep networks in DCCA.

Consider two views \(X_1\) and \(X_2\). Canonical Correlation Analysis seeks to find vectors \(a_1\) and \(a_2\) to maximize the correlation between \(X_1 a_1\) and \(X_2 a_2\).

w_

w[i] : nd-array List of the two weight matrices for projecting each view.

Type

list (length=2)

m_

m[i] : nd-array List of the means of the data in each view.

Type

list (length=2)

class mvlearn.embed.cca_loss(n_components, use_all_singular_values, device)

An implementation of the loss function of linear CCA as introduced in the original paper for DCCA 9. Details of how this loss is computed can be found in the paper or in the documentation for DCCA.

Parameters

• n_components (int (positive)) -- The output dimensionality of the CCA transformation.

• use_all_singular_values (boolean) -- Whether or not to use all the singular values in the loss calculation. If False, only use the top n_components singular values.

• device (torch.device object) -- The torch device being used in DCCA.

n_components_

The output dimensionality of the CCA transformation.

Type

int (positive)

use_all_singular_values_

Whether or not to use all the singular values in the loss calculation. If False, only use the top n_components singular values.

Type

boolean

device_

The torch device being used in DCCA.

Type

torch.device object

class mvlearn.embed.MlpNet(layer_sizes, input_size)

Multilayer perceptron implementation for fully connected network. Used by DCCA for the fully transformation of a single view before linear CCA. Extends torch.nn.Module.

Parameters

• layer_sizes (list of ints) -- The sizes of the layers of the deep network applied to view 1 before CCA. For example, if the input dimensionality is 256, and there is one hidden layer with 1024 units and the output dimensionality is 100 before applying CCA, layer_sizes1=[1024, 100].

• input_size (int (positive)) -- The dimensionality of the input vectors to the deep network.

layers_

The layers in the network.

Type

torch.nn.ModuleList object

Initializes internal Module state, shared by both nn.Module and ScriptModule.

class mvlearn.embed.DeepPairedNetworks(layer_sizes1, layer_sizes2, input_size1, input_size2, n_components, use_all_singular_values, device=device(type='cpu'))

A pair of deep networks for operating on the two views of data. Consists of two MlpNet objects for transforming 2 views of data in DCCA. Extends torch.nn.Module.

Parameters

• layer_sizes1 (list of ints) -- The sizes of the layers of the deep network applied to view 1 before CCA. For example, if the input dimensionality is 256, and there is one hidden layer with 1024 units and the output dimensionality is 100 before applying CCA, layer_sizes1=[1024, 100].

• layer_sizes2 (list of ints) -- The sizes of the layers of the deep network applied to view 2 before CCA. Does not need to have the same hidden layer architecture as layer_sizes1, but the final dimensionality must be the same.

• input_size1 (int (positive)) -- The dimensionality of the input vectors in view 1.

• input_size2 (int (positive)) -- The dimensionality of the input vectors in view 2.

• n_components (int (positive), default=2) -- The output dimensionality of the correlated projections. The deep network will transform the data to this size. If not specified, will be set to 2.

• use_all_singular_values (boolean (default=False)) -- Whether or not to use all the singular values in the CCA computation to calculate the loss. If False, only the top n_components singular values are used.

• device (string, default='cpu') -- The torch device for processing.

model1_

Deep network for view 1 transformation.

Type

MlpNet object

model2_

Deep network for view 2 transformation.

Type

MlpNet object

loss_

Loss function for the 2 view DCCA.

Type

cca_loss object

Initializes internal Module state, shared by both nn.Module and ScriptModule.

Dimension Selection

mvlearn.embed.select_dimension(X, n_components=None, n_elbows=2, threshold=None, return_likelihoods=False)

Generates profile likelihood from array based on Zhu and Godsie method 14. Elbows correspond to the optimal embedding dimension.

Parameters

• X (1d or 2d array-like) -- Input array generate profile likelihoods for. If 1d-array, it should be sorted in decreasing order. If 2d-array, shape should be (n_samples, n_features).

• n_components (int, optional, default: None.) -- Number of components to embed. If None, n_components = floor(log2(min(n_samples, n_features))). Ignored if X is 1d-array.

• n_elbows (int, optional, default: 2.) -- Number of likelihood elbows to return. Must be > 1.

• threshold (float, int, optional, default: None) -- If given, only consider the singular values that are > threshold. Must be >= 0.

• return_likelihoods (bool, optional, default: False) -- If True, returns the all likelihoods associated with each elbow.

Returns

• elbows (list) -- Elbows indicate subsequent optimal embedding dimensions. Number of elbows may be less than n_elbows if there are not enough singular values.

• sing_vals (list) -- The singular values associated with each elbow.

• likelihoods (list of array-like) -- Array of likelihoods of the corresponding to each elbow. Only returned if return_likelihoods is True.

References

13

Code from the https://github.com/neurodata/graspy package, reproduced and shared with permission.

14

Zhu, M. and Ghodsi, A., "Automatic dimensionality selection from the scree plot via the use of profile likelihood. Computational Statistics & Data Analysis." 51(2):918-930, 2006