Conditional Independence of Views on Multiview KMeans Clustering

The co-Expectation Maximization framework (and co-training), relies on the fundamental assumption that data views are conditionally independent. In this tutorial we test that assumption by examining the multiview k-means clustering algorithm on synthetic multiview datasets under different conditions related to independence between the views conditioned on true class labels.

In the following experiments, we will perform singleview kmeans clustering on two views separately and on them concatenated together. We also perform multiview clustering using the multiview algorithm. We will also compare the performance of multiview and singleview versions of kmeans clustering. We will evaluate the purity of the resulting clusters from each algorithm with respect to the class labels using the normalized mutual information metric.

# License: MIT

import warnings
import numpy as np
from scipy import special
import matplotlib.pyplot as plt
from sklearn.metrics import normalized_mutual_info_score as nmi_score
from sklearn.cluster import KMeans
from sklearn.datasets import fetch_covtype
from sklearn.manifold import TSNE
from mvlearn.cluster import MultiviewKMeans

warnings.filterwarnings("ignore")
RANDOM_SEED = 10

Artificial dataset with conditionally independent views

Here, we create an artificial dataset where the conditional independence assumption between views, given the true labels, is enforced. Our artificial dataset is derived from the forest covertypes dataset from the scikit-learn package. This dataset is comprised of 7 different classes, with with 54 different numerical features per sample. To create our artificial data, we will select 500 samples from each of the first 6 classes in the dataset, and from these, construct 3 artificial classes with 2 views each. <br>

def get_ci_data(num_samples=500):
    # Load in the vectorized news group data from scikit-learn package
    cov = fetch_covtype()
    all_data = np.array(cov.data)
    all_targets = np.array(cov.target)

    # Set class pairings as described in the multiview clustering paper
    view1_classes = [1, 2, 3]
    view2_classes = [4, 5, 6]

    # Create lists to hold data and labels for each of the classes across
    # 2 different views
    labels = [num for num in range(len(view1_classes))
              for _ in range(num_samples)]
    labels = np.array(labels)
    view1_data = list()
    view2_data = list()

    # Randomly sample items from each of the selected classes in view1
    for class_num in view1_classes:
        class_data = all_data[(all_targets == class_num)]
        indices = np.random.choice(class_data.shape[0], num_samples)
        view1_data.append(class_data[indices])
    view1_data = np.concatenate(view1_data)

    # Randomly sample items from each of the selected classes in view2
    for class_num in view2_classes:
        class_data = all_data[(all_targets == class_num)]
        indices = np.random.choice(class_data.shape[0], num_samples)
        view2_data.append(class_data[indices])
    view2_data = np.concatenate(view2_data)

    # Shuffle and normalize vectors
    shuffled_inds = np.random.permutation(num_samples * len(view1_classes))
    view1_data = np.vstack(view1_data)
    view2_data = np.vstack(view2_data)
    view1_data = view1_data[shuffled_inds]
    view2_data = view2_data[shuffled_inds]
    magnitudes1 = np.linalg.norm(view1_data, axis=0)
    magnitudes2 = np.linalg.norm(view2_data, axis=0)
    magnitudes1[magnitudes1 == 0] = 1
    magnitudes2[magnitudes2 == 0] = 1
    magnitudes1 = magnitudes1.reshape((1, -1))
    magnitudes2 = magnitudes2.reshape((1, -1))
    view1_data /= magnitudes1
    view2_data /= magnitudes2
    labels = labels[shuffled_inds]
    return [view1_data, view2_data], labels


def perform_clustering(seed, m_data, labels, n_clusters):
    # Singleview kmeans clustering
    # Cluster each view separately
    s_kmeans = KMeans(n_clusters=n_clusters, random_state=seed, n_init=100)
    s_clusters_v1 = s_kmeans.fit_predict(m_data[0])
    s_clusters_v2 = s_kmeans.fit_predict(m_data[1])

    # Concatenate the multiple views into a single view
    s_data = np.hstack(m_data)
    s_clusters = s_kmeans.fit_predict(s_data)

    # Compute nmi between true class labels and singleview cluster labels
    s_nmi_v1 = nmi_score(labels, s_clusters_v1)
    s_nmi_v2 = nmi_score(labels, s_clusters_v2)
    s_nmi = nmi_score(labels, s_clusters)
    print('Singleview View 1 NMI Score: {0:.3f}\n'.format(s_nmi_v1))
    print('Singleview View 2 NMI Score: {0:.3f}\n'.format(s_nmi_v2))
    print('Singleview Concatenated NMI Score: {0:.3f}\n'.format(s_nmi))

    # Multiview kmeans clustering

    # Use the MultiviewKMeans instance to cluster the data
    m_kmeans = MultiviewKMeans(n_clusters=n_clusters,
                               n_init=100, random_state=seed)
    m_clusters = m_kmeans.fit_predict(m_data)

    # Compute nmi between true class labels and multiview cluster labels
    m_nmi = nmi_score(labels, m_clusters)
    print('Multiview NMI Score: {0:.3f}\n'.format(m_nmi))

    return m_clusters


def display_plots(pre_title, data, labels):
    # plot the views
    fig, ax = plt.subplots(1, 2, figsize=(14, 5))
    dot_size = 10
    ax[0].scatter(new_data[0][:, 0], new_data[0][:, 1], c=labels, s=dot_size)
    ax[0].set_title(pre_title + ' View 1')
    ax[0].axes.get_xaxis().set_visible(False)
    ax[0].axes.get_yaxis().set_visible(False)

    ax[1].scatter(new_data[1][:, 0], new_data[1][:, 1], c=labels, s=dot_size)
    ax[1].set_title(pre_title + ' View 2')
    ax[1].axes.get_xaxis().set_visible(False)
    ax[1].axes.get_yaxis().set_visible(False)

    plt.show()

Comparing the performance with conditionally independent views

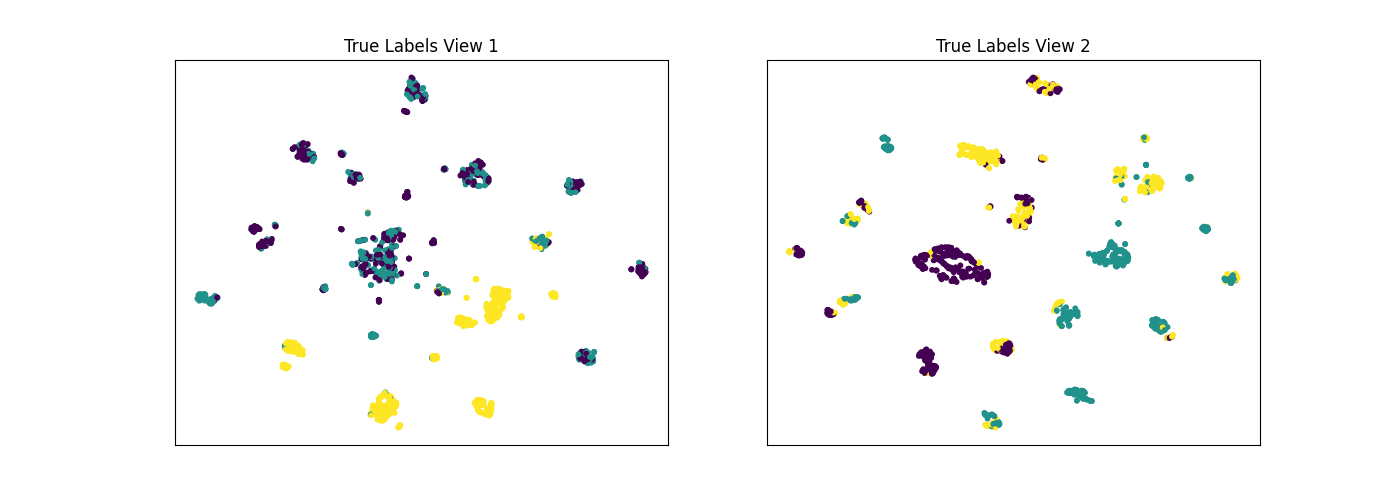
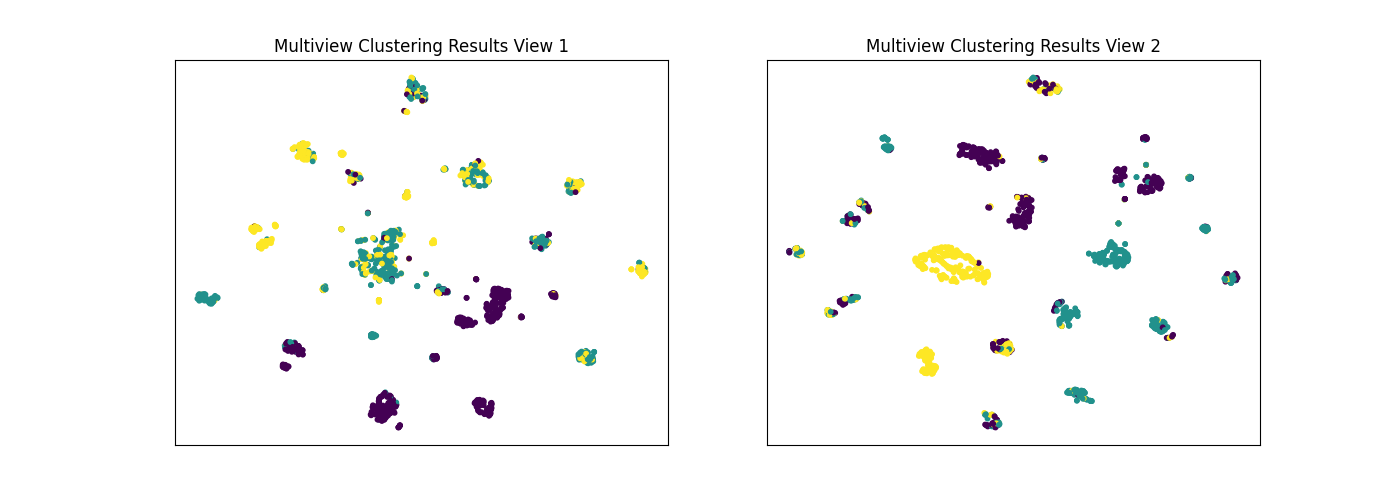
The co-Expectation Maximization framework (and co-training), relies on the fundamental assumption that data views are conditionally independent. If all views are informative and conditionally independent, then Multiview KMeans is expected to produce higher quality clusters than Singleview KMeans, for either view or for both views concatenated together. Here, we will evaluate the quality of clusters by using the normalized mutual information metric, which is essentially a measure of the purity of clusters with respect to the true underlying class labels.

As we see below, Multiview KMeans produces clusters with higher purity than Singleview KMeans across a range of values for the n_clusters parameter for data with complex and informative views, which is consistent with some of the results from the original Multiview clustering paper.

data, labels = get_ci_data()
m_clusters = perform_clustering(RANDOM_SEED, data, labels, 3)

# Running TSNE to display clustering results via low dimensional embedding
tsne = TSNE()
new_data = list()
new_data.append(tsne.fit_transform(data[0]))
new_data.append(tsne.fit_transform(data[1]))
display_plots('True Labels', new_data, labels)
display_plots('Multiview Clustering Results', new_data, m_clusters)

• 
• 

Out:

Singleview View 1 NMI Score: 0.323

Singleview View 2 NMI Score: 0.504

Singleview Concatenated NMI Score: 0.422

Multiview NMI Score: 0.609

Artificial dataset with conditionally dependent views

Here, we create an artificial dataset where the conditional independence assumption between views, given the true labels, is violated. We again derive our dataset from the forest covertypes dataset from sklearn. However, this time, we use only the first 3 classes of the dataset, which will correspond to the 3 clusters for view 1. To produce view 2, we will apply a simple nonlinear transformation to view 1 using the logistic function, and we will apply a negligible amount of noise to the second view to avoid convergence issues. This will result in a dataset where the correspondance between views is very high.

def get_cd_data(num_samples=500):
    # Load in the vectorized news group data from scikit-learn package
    cov = fetch_covtype()
    all_data = np.array(cov.data)
    all_targets = np.array(cov.target)

    # Set class pairings as described in the multiview clustering paper
    view1_classes = [1, 2, 3]

    # Create lists to hold data and labels for each of the classes across
    # 2 different views
    labels = [num for num in range(len(view1_classes))
              for _ in range(num_samples)]
    labels = np.array(labels)
    view1_data = list()
    view2_data = list()

    # Randomly sample 500 items from each of the selected classes in view1
    for class_num in view1_classes:
        class_data = all_data[(all_targets == class_num)]
        indices = np.random.choice(class_data.shape[0], num_samples)
        view1_data.append(class_data[indices])
    view1_data = np.concatenate(view1_data)

    # Construct view 2 by applying a nonlinear transformation
    # to data from view 1 comprised of a linear transformation
    # and a logistic nonlinearity
    t_mat = np.random.random((view1_data.shape[1], 50))
    noise = 0.005 - 0.01*np.random.random((view1_data.shape[1], 50))
    t_mat *= noise
    transformed = view1_data @ t_mat
    view2_data = special.expit(transformed)

    # Shuffle and normalize vectors
    shuffled_inds = np.random.permutation(num_samples * len(view1_classes))
    view1_data = np.vstack(view1_data)
    view2_data = np.vstack(view2_data)
    view1_data = view1_data[shuffled_inds]
    view2_data = view2_data[shuffled_inds]
    magnitudes1 = np.linalg.norm(view1_data, axis=0)
    magnitudes2 = np.linalg.norm(view2_data, axis=0)
    magnitudes1[magnitudes1 == 0] = 1
    magnitudes2[magnitudes2 == 0] = 1
    magnitudes1 = magnitudes1.reshape((1, -1))
    magnitudes2 = magnitudes2.reshape((1, -1))
    view1_data /= magnitudes1
    view2_data /= magnitudes2
    labels = labels[shuffled_inds]
    return [view1_data, view2_data], labels

Comparing the performance with conditionally dependent views

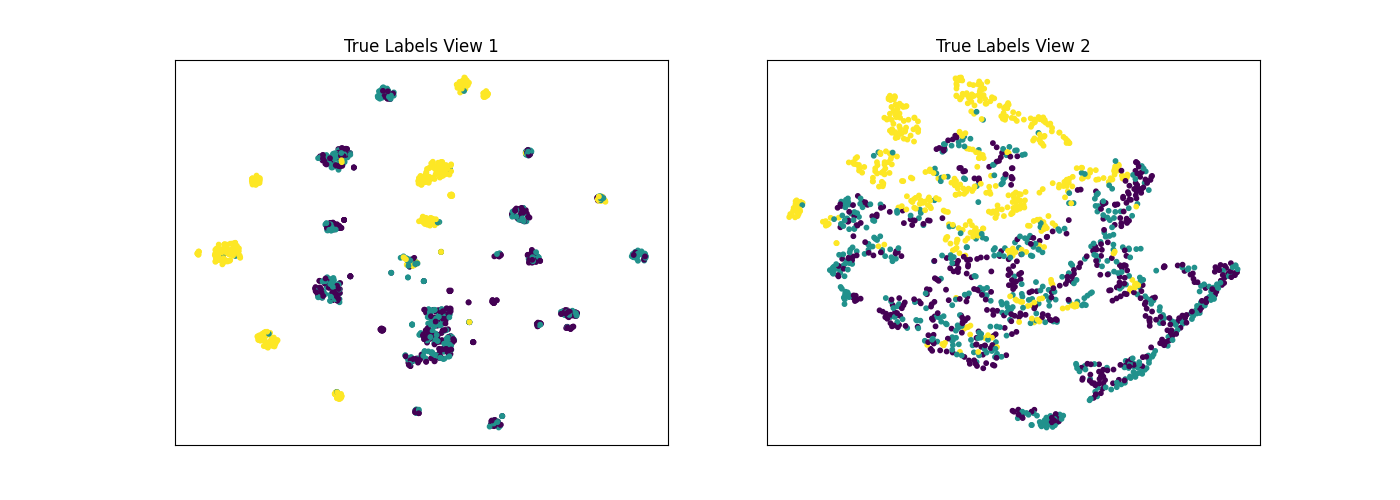
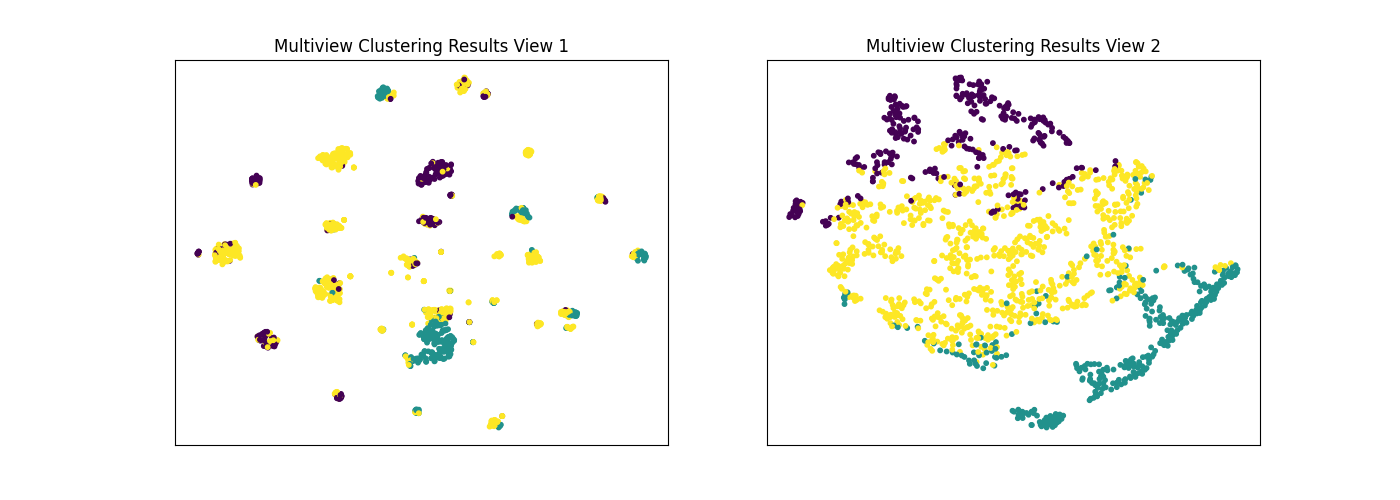
As mentioned before co-Expectation Maximization framework (and co-training), relies on the fundamental assumption that data views are conditionally independent. Here, we will again compare the performance of singleview and multiview kmeans clustering using the same methods as before, but on our conditionally dependent dataset.

As we see below, Multiview KMeans does not beat the best Singleview clustering performance with respect to purity, since that the views are conditionally dependent.

data, labels = get_cd_data()
m_clusters = perform_clustering(RANDOM_SEED, data, labels, 3)

# Running TSNE to display clustering results via low dimensional embedding
tsne = TSNE()
new_data = list()
new_data.append(tsne.fit_transform(data[0]))
new_data.append(tsne.fit_transform(data[1]))
display_plots('True Labels', new_data, labels)
display_plots('Multiview Clustering Results', new_data, m_clusters)

• 
• 

Out:

Singleview View 1 NMI Score: 0.330

Singleview View 2 NMI Score: 0.107

Singleview Concatenated NMI Score: 0.259

Multiview NMI Score: 0.234